Teorema de Norton

El Teorema de Norton

Este es otro útil teorema para analizar circuitos eléctricos como lo es el teorema de Thevenin, el cual reduce circuitos complejos en circuitos equivalentes mas simples. La principal diferencia entre los dos teoremas es que el teorema de Thevenin provee un fuente de voltaje equivalente y  una resistencia en serie equivalente, mientras que el teorema de Norton provee una fuente de corriente equivalente y una resistencia en paralelo equivalente.

Pasos simples para analizar un circuito eléctrico mediante el teorema de norton

1. Ponemos en corto la resistencia
2. Medimos la corriente, esta es la corriente de Norton
3. Abrimos las fuentes de corriente, ponemos en corto las fuentes de voltaje y abrimos la resistencia.
4. Medimos la resistencia, esta es la resistencia de Norton
5. Ahora rediseñamos el circuito con la corriente medida en el paso 2 como una fuente de corriente y la resistencia medida en el paso 4 como una resistencia en paralelo, y finalmente conectamos la resistencia que habíamos removido en el paso 3. Este es circuito equivalente de Norton.
6. Ahora encontramos la corriente que fluye en el circuito, el voltaje y la resistencia mediante la regla de la división de la corriente  I_L = I_N / (R_N / (R_N+ R_L))

Ejercicio

Encontrar la resistencia de norton y la corriente de norton.

Figura 1

Paso 1

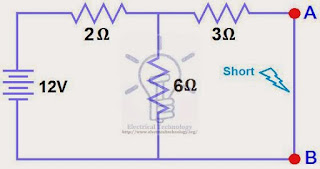
Ponemos en corto la resistencia de 1.5Ohm como se muestra en la figura 2

Figura 2

Paso 2

Medimos la corriente del corto, esta será la corriente de Norton. Hemos puesto en corto los terminales A y B para determinar la corriente de Norton. Las resistencias de 6Ohm y 3Ohm están ahora en paralelo y estas a su vez están en serie con la de 2Ohm, por ende la resistencia total del circuito es:

2Ω + (6Ω || 3Ω) 

R_T = 2Ω + [(3Ω x 6Ω) / (3Ω + 6Ω)] → I_T= 2Ω + 2Ω = 4Ω.

R_T = 4Ω

I_T = V / R_T

I_T = 12V / 4Ω

I_T = 3A..

I_SC = I_N = 3A x [(6Ω / (3Ω + 6Ω)] = 2A.

I_SC= I_N = 2A.

Figura 3

Paso 3

Abrir las fuentes de corriente, poner en corto las fuentes de voltaje y abrir la resistencia. Figura(4)

Figura 4

Paso 4

Medimos la resistencia del circuito abierto, esta será la resistencia de Norton.

Se ha reducido la fuente de 12V a cero, lo que es equivalente a remplazarla por un corto.

3Ω + (6Ω || 2Ω) 

R_N = 3Ω + [(6Ω x 2Ω) / (6Ω + 2Ω)]

R_N = 3Ω + 1.5Ω

R_N = 4.5Ω

Figura 5

Paso 5

Conectamos la resistencia de Norton en paralelo con la fuente de corriente y luego reconectamos la resistencia previamente desconectada en la figura 4.

Figura 6 (Circuito equivalente de Norton)

Paso 6

Ahora el ultimo paso, calculamos la corriente y el voltaje que fluye a través de la resistencia mediante la ley de Ohm como se muestra en la figura 7

I_L = I_N x [R_N / (R_N+ R_L)]

= 2A x (4.5Ω /4.5Ω +1.5Ω) → = 1.5A

I_L = 1. 5A

V_L = I_L x R_L

V_L = 1.5A x 1.5Ω

V_L= 2.25V

Ahora comparemos este simple circuito con el original de la figura 1, podemos ver cuan sencillo será medir o calcular la corriente y el voltaje a través de las diferentes resistencias, gracias al teorema de Norton.